Jak se bránit proti rozhodnutí v rámci Matematiky – vyšší úrovně obtížnosti
Milí maturanti,
kteří jste řešili test Matematika – vyšší úroveň obtížnosti.
Chci Vám předvést, jak se bránit nesprávnému posouzení Vaší odpovědi v úloze 19 (grafy funkcí).
V ní jste měli najít v nabídce graf funkce g=1/f .
Trvám na tom, že jste během zkoušky neměli čas poznat, zda je správnou odpovědí C, nebo E.
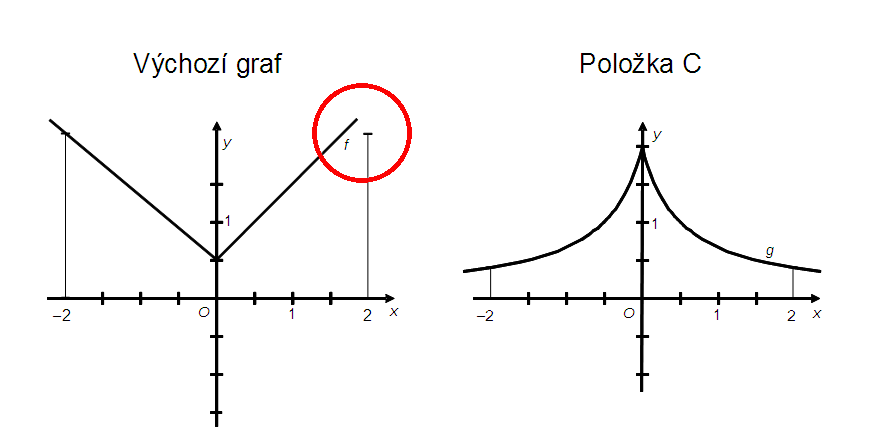
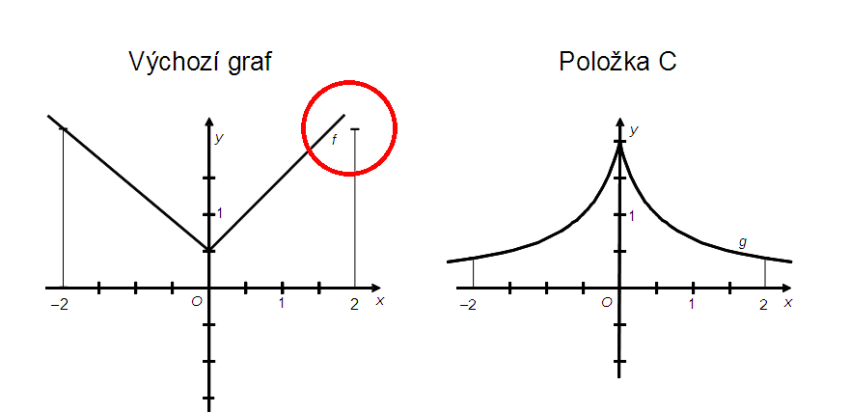
Řada z vás jistě při pohledu na výchozí graf funkce f uvažovala, zda je či není symetrický podle osy y. Mně trvalo asi půl hodiny (a musel jsem použít 4násobné zvětšení), abych ukázal, že není. Nijak jsem neměnil tvar a umístění křivek, pouze jsem odsunul o něco doprava označení osy x. Z obrázku vyplývá, že (i když to tak autor úlohy nezamýšlel) správnou odpovědí je položka E – a nikoli C, jak uvádí Cermat. Důkaz je snadný.
Podle Cermatu je správnou odpovědí C, tedy vztah g=1/f prý opravdu platí.
Jak každý vidí na pravém obrázku, g(–2) = g(2). Mělo by tedy rovněž platit f(–2) = f(2). To však zjevně není pravda (viz levý obrázek). Protože položky A, B a D nabídky lze vyloučit ještě snadněji, je správnou odpovědí položka E – žádný z uvedených grafů.
Matematika je jediný obor, v němž je možno takhle snadno nezvratně dokázat, že někdo nemá pravdu.
Cermat a jeho ředitel Ing. Pavel Zelený tedy nemají pravdu, když tvrdí, že správnou odpovědí je C.
Podklad ke stažení ZDE.
Praha, 18. května 2012
RNDr. Oldřich Botlík, CSc.