Oldřich Botlík: V zadání maturitního testu z matematiky byla chyba

Publikujeme text Oldřicha Botlíka, který analyzuje jednu z maturitních úloh z matematiky a dokazuje, že neplatí tvrzení ministerstva školství o tom, že všechny úlohy jsou formulovány jednoznačně a mají jednoznačná řešení.

Podle tiskové zprávy MŠMT potvrdila Nezávislá odborná komise pro maturitní zkoušku mimo jiné, že všechny úlohy maturitních testů jsou formulovány jednoznačně a mají jednoznačně správná řešení uvedená v klíči správných řešení. Podívejme se tedy na úlohu 11 testu z matematiky.

Řešením úlohy 11 je podle klíče úhel 248º, ale nikoli také úhel 112º.

Vzhledem k řešení v klíči ovšem nebyla úloha správně zadaná. Úhel je podle definice část roviny mezi dvěma polopřímkami vycházejícími ze stejného bodu – nikoli číslo. Nic tedy nebrání tomu, aby dva různé úhly měly stejnou velikost. V rovině existuje nekonečně mnoho různých úhlů o velikosti 112°. Těm, kteří tuhle část matematiky už zapomněli, nabízím srozumitelnou analogii.

Pepa může být vysoký nejen 170 cm, ale také 180 cm – i když je to rovněž výška Franty a Pepa není Franta. Kdyby zadání úlohy 11 začínalo slovy Pro dva různě velké úhly…, měla by opravdu jediné řešení. Obdobně, když bude zadání úlohy o lidech začínat slovy Pro dva různě vysoké lidi…, vyloučí u Pepy výšku 180 cm. Z chyby se navíc Cermat usvědčil sám. V jiné letošní úloze (obrázek níže) totiž správně použil termín „úhel“, když šlo o polohu různých částí roviny, a termín „velikost úhlu“, když šlo o to, jak jsou velké. Proč by tedy žáci, zvláště ti slabší, případně hodně přemýšliví, měli v úloze 11 najednou začít chápat „úhel“ v rozporu s definicí výhradně jako „velikost úhlu“?

K čemu mohlo zadání vést

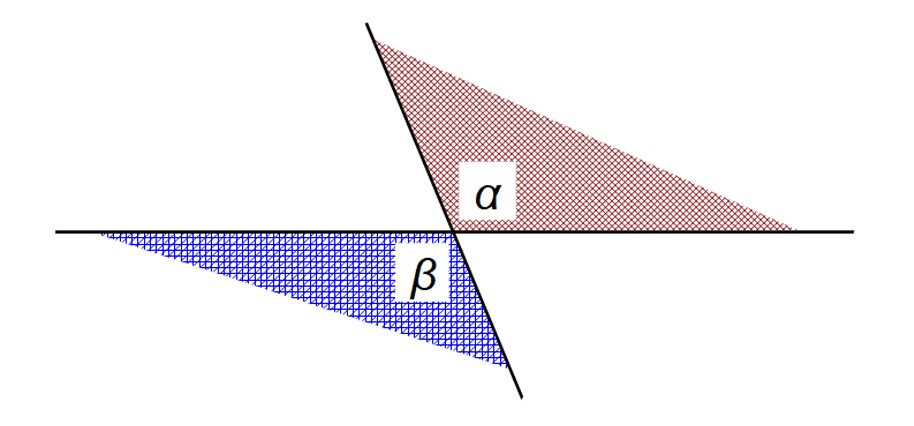
Řešení β = 248º nepochybně vyhovuje zadání Cermatu. Žáci, kteří se řídili zadáním úlohy, ovšem správnou úvahou dospěli také k hodnotě β = 112º. Jak, to lze snadno vysvětlit. Úhly α = 112º, β = 112º na obrázku níže jsou totiž nepochybně různé, jak zadání požaduje, neboť leží každý jinde, mezi různými polopřímkami. Velikost úhlu β není menší než 0º ani větší než 360º a samozřejmě platí rovněž vztah cos α = cos β.

Kolik žáků uvedlo druhé řešení, případně obě?

V Cermatu znají jejich přesný počet, já si myslím, že jich je nejméně několik desítek, možná stovek. Veřejnost to ale nyní zjistit nemůže, neboť ke zpřístupnění anonymizovaných dat, agregovaných dat a grafických interpretací dat má podle publikačního kalendáře dojít „do 31. července 2019“. Právě kvůli podobným situacím by měl ovšem Cermat zveřejňovat četnosti odpovědí žáků (včetně četností odpovědí „podezřelých“) co nejdříve, tedy současně s klíčem správných řešení.

Tak by se totiž měla chovat instituce, která chce navrátit maturitní zkoušce prestiž. Maturanti mohou informace využít třeba k tomu, aby upustili od odvolání. Nebo naopak k tomu, aby je připravili co nejlépe. Pochybné vítězství „Kombajnu“ nad žáky, dosažené díky neopodstatněné informační převaze Cermatu a popírání nedostatků v testech, je ale pokaždé vítězstvím Pyrrhovým. Jde-li ministru Plagovi o vzájemnou důvěru v resortu, neměl by podobné praktiky trpět.

Především neškodit

Proč je takové vítězství pochybné? Pokud byť jen jediný žák uvedl jako výsledek hodnotu 112º, případně obě hodnoty 112º a 248º, měl podle mého názoru dostat 1 bod stejně jako žáci, kteří uvedli pouze hodnotu 248º. Jeho cesta k takovému výsledku je totiž správná.

Plošné testování je charakterizováno mimo jiné tím, že žák a hodnotitel jeho odpovědí v testu nemůžou vysvětlit případné nejasnosti jeden druhému tak, jako to jde mezi žákem a učitelem ve škole. Proto by hodnotitelé měli hledat přijatelná vysvětlení nečekaných odpovědí žáků – nikoli zarputile trvat na svém. Cermat hodnotu 112º nevyloučil a žáci neskládají zkoušku ze schopnosti empatie. Tu měl mít autor úlohy. Jestliže se mezi výsledky objevila také hodnota 112º, měli se v Cermatu zamyslet a hledat pro ni vysvětlení. V podobné situaci (jde o významnou zkoušku, která často rozhoduje o dalších životních osudech žáků) má Cermat projevit velkorysost a nadhled. Aby neškodil.

Ti žáci, kterým byl 1 bod upřen a jde jim o spravedlnost nebo o to, aby nepropadli, se nyní budou muset domáhat jiného hodnocení své odpovědi prostřednictvím odvolání, případně správní žalobou na ministerstvo školství (pokud ministerstvo nevyhoví jejich odvolání). Zbytečně to zatěžuje všechny zúčastněné. V matematice se tvrzení dokazují a Cermat nemůže dokázat, že hodnota 112º není řešením jeho úlohy. Ačkoli oceňuji, že letos poprvé zveřejnil vzorová řešení, nepostupoval v tomto případě dost důkladně.

Až v Cermatu začnou přistupovat k vlastním úlohám s pokorou a k odpovědím maturantů s empatií, rád si podobné články odpustím. Zatím však státní maturita každoročně poškozuje nevinné žáky, jimž stát navíc upírá informace, které mohou využít ke své obraně. A s tím se smířit nehodlám.