Oldřich Botlík: Každý z obou správných výsledků úlohy 11 mohli maturanti napsat bez porozumění

Přečtěte si text Oldřicha Botlíka, který popisuje, v čem spočívá potíž s úlohou 11 didaktického testu z matematiky v rámci letošních maturit. Kolem nejednoznačného zadání úlohy se již víc než týden vede diskuse, kterou můžete sledovat ZDE.

Nejprve několik slov k nejednoznačnosti zadání. Představme si na chvíli, že Cermat zadal maturantům úkol napsat, co je na následujícím obrázku.

Někteří maturanti napsali „dvě tváře“. Jiní napsali „váza“. Někteří možná dokonce napsali „dvě tváře a váza“.

Cermat viděl na obrázku jenom dvě tváře, a tak přidělil bod těm maturantům, kteří viděli totéž. Ostatním nic. Já jsem potom upozornil, že na obrázku je obojí. A že podle mého názoru by měli dostat bod také někteří další: ti maturanti, kteří napsali „dvě tváře a váza“, a rovněž maturanti, kteří napsali jen „váza“.

Analogie podle mého názoru docela pěkně popisuje, v čem byl zpočátku problém. To, co člověk při pozorování obrázku rozpozná nejdřív, například dvě tváře, se totiž v jeho mozku posílí. Zbytek obrázku ztratí vlastní smysl a stane se pouhým pozadím rozpoznaného objektu. Vrátit tomuto „pozadí“ jinou interpretaci bývá potom obtížné, někdo to dokonce ani nedokáže. To je důvodem, proč lidé optické klamy vymýšlejí a baví se jimi.

O úloze 11 maturitního testu z matematiky se diskutuje několik dní a zdá se mi, že většina lidí už tam vidí jak „dvě tváře“, tak „vázu“. Prostě uznali, že pokud chtěl Cermat vyloučit výsledek 112º, měl v zadání napsat „pro dva různě velké úhly“ – nikoli pouze „pro dva různé úhly“.

Nyní k tomu, jak mohli žáci dospět k výsledku 112º, případně k výsledku 248º. V diskusích se teď objevují argumenty, proč by měl být 1 bod přidán pouze těm žákům, kteří uvedli obě hodnoty, tedy 112º a 248º. Žáci, kteří odpověděli pouze 112º, prý podstatě úlohy nerozumějí. To může být pravda – byl jedinou hodnotou v zadání, která mohla „kandidovat“ na správnou odpověď, a někteří žáci v nesnázích tak opravdu postupují. Když nevědí, prostě si aspoň něco tipnou. Musím se ale zeptat, kde tito diskutující berou jistotu, že podstatě úlohy rozumějí všichni autoři odpovědi 248º, jejichž 1 bod nikdo nezpochybňuje.

Sám jsem v projektu Kalibro dlouhých 25 let ukazoval učitelům matematiky cesty, které dovedly jejich žáky k chybným výsledkům. Vím tedy, čeho všeho jsou žáci schopni, když se dostanou do úzkých: například vezmou nějaká dvě čísla vyskytující se v zadání, a aniž by čemukoli rozuměli, odečtou menší od většího a výsledek zapíšou do záznamového archu. V zadání úlohy 11 byla čísla 360 a 112, jejichž rozdíl 360 – 112 je roven hodnotě 248. Takhle „naslepo“ možná postupovalo řádově stejně žáků, jako bylo těch, kteří podobně „naslepo“ uvedli odpověď 112º. Poznalo by se to, kdyby zadání nepožadovalo rovnost cos(alfa)=cos(beta), nýbrž rovnost sin(alfa)=sin(beta). Rovnost sin(alfa)=sin(248º) totiž neplatí, ovšem žáci by navzdory tomu stejně uváděli hodnotu 248º jako výsledek. Vysvětlení je prosté: odečítání na jednotkové kružnici nerozumějí ani v případě funkce sinus (neboť princip je u sinu podobný jako u kosinu), a tak by i tentokrát postupovali „naslepo“.

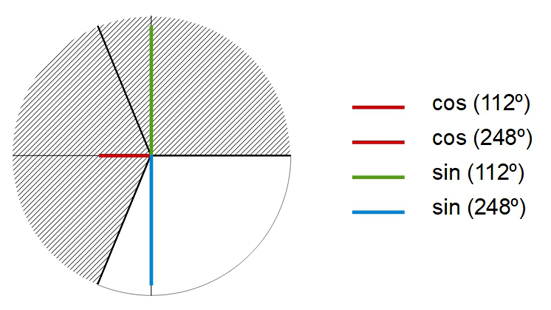
Jenomže úloha s rovností sin(alfa)=sin(beta) by tyto žáky odhalila. K jejímu správnému výsledku 68º (druhý výsledek 112º zůstává správný i v ní) totiž cesta „naslepo“ 360 – 112 nevede. Úloha 11 tedy měla nejen nejednoznačné zadání, ale byla rovněž nevhodně konstruována. Umožnila snadno uspět žákům, kteří si neosvojili to, co nejspíš měla úloha ověřit: zda pochopili, jak se hodnoty kosinu odečítají na jednotkové kružnici.

Závěr: Z přísně matematického hlediska si zaslouží 1 bod pouze ti žáci, kteří v odpovědi uvedli obě hodnoty 112º a 248º. To by ovšem nejspíš byla katastrofa neodpovídající úrovni znalostí žáků. A zavinil by ji Cermat – nikoli maturanti. Kvůli dodržení zásady „Především neškodit“ je ale potom nutné udělit bod také všem žákům, kteří uvedli pouze jednu z obou těchto hodnot (a žádnou další). Jinak by vznikla další nespravedlnost. Úloha 11 totiž nepožadovala žádné zdůvodnění a ze samotného čísla není možné prokázat, že k němu určitý žák dospěl „naslepo“. Jak u výsledku 112º, tak u výsledku 248º ale zcela jistě existuje významná část žáků, kteří k němu „naslepo“ dospěli. Nechápou sice, jak se hodnoty funkce cos na jednotkové kružnici odečítají, ovšem Cermat připravil úlohu tak nešikovně, že tyto žáky nelze najít.

Jinak řečeno, úloha neověřila, co nejspíš ověřit měla. V posudku Nezávislé odborné komise MŠMT pro posouzení maturitního testu z matematiky se přesto dočteme: Všechny úlohy v didaktickém testu z matematiky v jarním zkušebním období 2019 i didaktický test jsou konstrukčně v pořádku. Všechny úlohy jsou formulovány jednoznačně, mají jednoznačně správná řešení uvedená v klíči správných řešení.

Vypadá to, že si z nás dělají legraci.